(DC) – direct current
Cells and batteries provide an electrical current which always flows around the circuit in the same direct, this is called direct current (DC).

(AC) – alternating current
In the UK mains electricity is supplied at about 230 volts and is supplied as (AC) or alternating current. This means the current flows in one direction then the other around the circuit. The current constantly changes direction (alternates) and so it is called (ac) alternating current. In the UK the frequency of mains electricity is 50 Hz, this means 50 cycles in one second.

AC signals
We can use an oscilloscope to represent an AC signal.
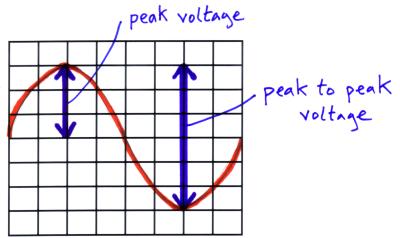
We can use the oscilloscope trace as a voltmeter if we know what the y-gain is set to on the oscilloscope. Using the diagram above and knowing that the Y-gain was set to 10 V / div we can work out that;
- the peak to peak voltage = 6 squares from the highest point to the lowest and each square is worth 10V. So the peak to peak voltage = 60 V.
- the peak voltage ( Vo )= half the peak to peak voltage = 60 / 2 = 30 V
Once we know the peak voltage ( Vo ) and the resistance (R) in the circuit we can calculate the peak current ( Io ) using the equation V=IR.
Root mean square (rms) values
As the p.d. and current are varying continuously in an AC signal we need to represent an average value for p.d. and current.
The root mean square values of p.d. ( Vrms ) and current ( Irms) represent the effective value of the p.d. and current in an AC circuit.
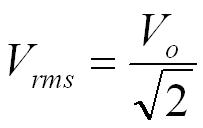
- Vrms = root mean square potential difference in volts, V
- Vo = peak voltage in volts, V
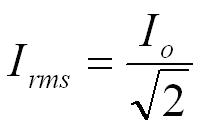
- I = root mean square current in amperes, A
- Io= peak current in amperes, A



