The electromotive force (e) or e.m.f. is the energy provided by a cell or battery per coulomb of charge passing through it, it is measured in volts (V). It is equal to the potential difference across the terminals of the cell when no current is flowing.
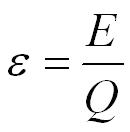
- e = electromotive force in volts, V
- E = energy in joules, J
- Q = charge in coulombs, C
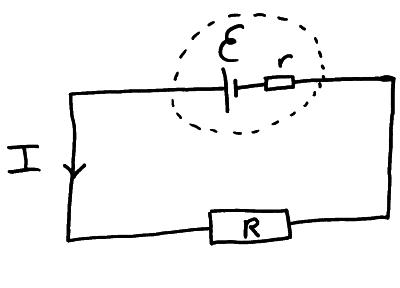
Batteries and cells have an internal resistance (r) which is measures in ohm’s (W). When electricity flows round a circuit the internal resistance of the cell itself resists the flow of current and so thermal (heat) energy is wasted in the cell itself.
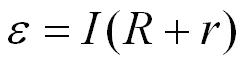
- e = electromotive force in volts, V
- I = current in amperes, A
- R = resistance of the load in the circuit in ohms, W
- r = internal resistance of the cell in ohms, W
We can rearrange the above equation;
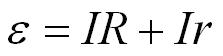
and then to
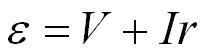
In this equation (V) appears which is the terminal potential difference, measured in volts (V). This is the potential difference across the terminals of the cell when current is flowing in the circuit, it is always less than the e.m.f. of the cell.
Example;
Q1) The p.d. across the terminals of a cell is 3.0 volts when it is not connected to a circuit and no current is flowing. When the cell is connected to a circuit and a current of 0.37 A is flowing the terminal p.d. falls to 2.8 V. What is the internal resistance of the cell?
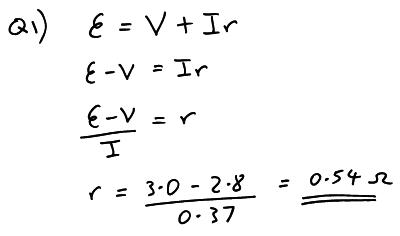
A graph of terminal p.d. against current
If we plot a graph of terminal potential difference (V) against the current in the circuit (I) we get a straight line with a negative gradient.
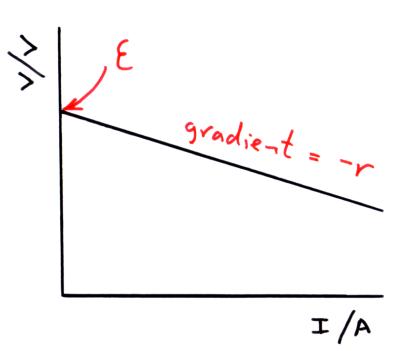
We can them rearrange the e.m.f. equation from above to match the general experesion for a straight line, y = mx +c.

We can see from the red boxes above that;
- the intercept on the y-axis is equal to the e.m.f. of the cell
- the gradient of the graph is equal to -r where r is the internal resistance of the cell.



