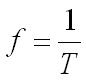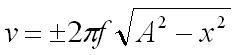Click here for questions & homework on SHM.
Objects can oscillate in all sorts of ways but a really important form of oscillation is SHM or Simple Harmonic Motion.
An object is undergoing simple harmonic motion (SHM) if;
- the acceleration of the object is directly proportional to its displacement from its equilibrium position.
- the acceleration is always directed towards the equilibrium position.
The frequency (f) of an oscillation is measure in hertz (Hz) it is the number of oscillations per second. The time for one oscillation is called the period (T) it is measured in seconds.
Acceleration – we can calculate the acceleration of the object at any point in it’s oscillation using the equation below.
In this equation; a = acceleration in ms-2, f = frequency in Hz, x = displacement from the central position in m.
Displacement – When using the equation below your calculator must be in radians not degrees ! we can calculate the displacement of the object at any point in it’s oscillation using the equation below.
The terms in this equation are the same as the equations above. The extra terms in this equation are: A = the amplitude (maximum displacement) in m, t = the time since the oscillation began in s.
Velocity– we can calculate the velocity of the object at any point in it’s oscillation using the equation below.
The terms in this equation are the same as the equations above. The extra term in this equation is: v = the velocity in ms-1.
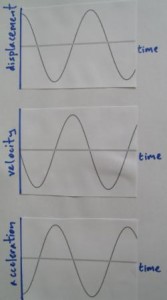
SHM graphs
When we plot the displacement, velocity and acceleration during SHM against time we get the graphs below.
The velocity equation simplifies to the equation below when we just want to know the maximum speed.
The acceleration equation simplifies to the equation below when we just want to know the maximum acceleration.
![]()
Time period of a mass-spring system
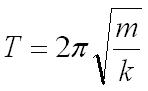

Time period of a Pendulum
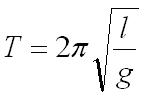
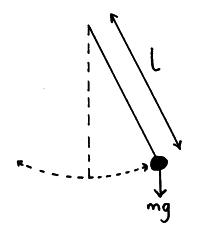
SHM and Energy
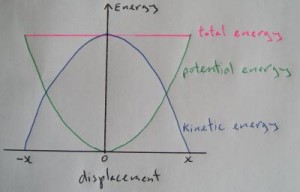
For a pendulum undergoing SHM energy is being transferred back and forth between kinetic energy and potential energy. The total energy remains the same and is equal to kinetic energy + potential energy (see graph below).
Links to other pages;