Nuclear Radius

Closest distance of approach of an alpha particle

We can estimate the radius of a nucleus by firing an alpha particle directly at the nucleus. The alpha particle will lose kinetic energy as it approaches the nucleus and gain potential energy due to the electric field because of the electrostatic repulsion between the positively charged nucleus and the positively charged alpha particle.

We can then work out the closest distance of approach of the alpha particle to the nucleus.

loss in kinetic energy E_k = gain in potential energy by the field E_p

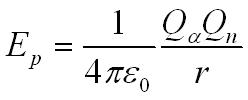
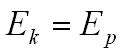
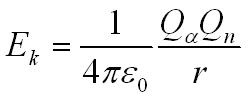
These experiments show the nucleus must be smaller than about 10^-14m

Electron diffraction

We can achieve a better estimate of the size of a nucleus by looking at the angle q_m to the first minimum when electrons are diffracted by a foil target.

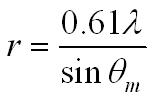
where l is the wavelength of the electrons.

This technique shows the nucleus to have a radius of about 10^-15 m

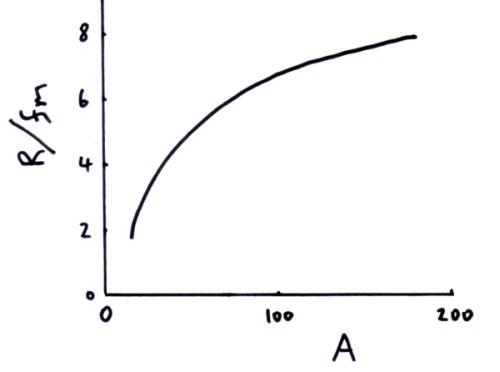
Nuclear radius and nucleon number

From experimental data the equation below has been derived.

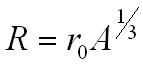
R = nuclear radius in metres (m)
r₀ = is the radius of a nucleon approx 1.3 fm
A = nucleon number

Nuclear Density

By assuming the nucleus to be a sphere we can calculate the density of the nucleus.

V = volume in m³
R = nuclear radius in m

Using the equation for nuclear radius from the section above

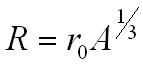
A = nucleon number

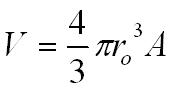
The mass (M) of the whole nucleus is the mass of a nucleon (m) multiplied by the number of nucleons (A)

Mass M = Am

Density can be found using the equation below;

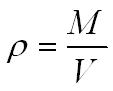
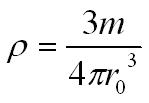
The nuclear density of a nucleus is approx 1.8 x 10¹⁷ kgm^-3