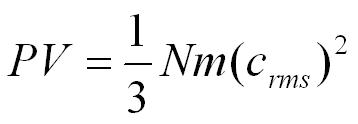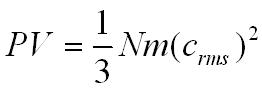
Think about a single molecule moving towards the end of a box. The box is a cube so all sides are of length (L). The molecule has a mass (m) and a velocity (v1). Therefore the molecule has a momentum of mv1.
momentum = mv1
When it collides with the end of the box in an elastic collision it goes back in the exactly opposite direction but with the same velocity. Its moment is now -mv1.
change in momentum = mv1– (-mv1) = 2mv1
To get back to the same side of the box it will have to travel to the other end of the box (a distance of L) and back (a distance of L) so the total distance travelled will be 2L.
distance travelled = 2L
the time for this to happen (t) will given by time = distance /speed
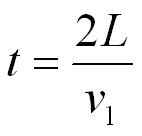
The number of collisions with the wall per second will be 1/t
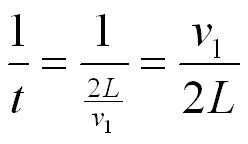
The rate of change of momentum is equal to the change in momentum multiplied by the number of collisions with the wall per second.

Newton’s 2nd Law tells us the force exerted on the wall by the molecule is equal to the rate of change of momentum.
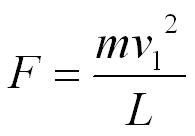
We can now use the equation pressure = force / area. The area of the end of the box is L2.
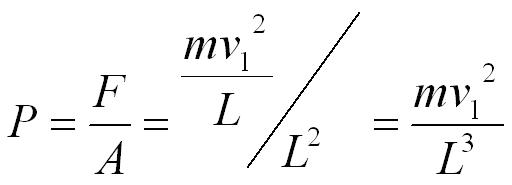
The volume of the box (V) is equal to L3, so we can substitute V into the equation.
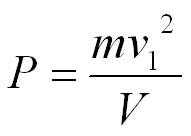
This is the pressure excerted by 1 molecule but we can multiply by the number of molecules in the box (N).
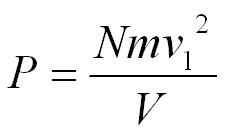
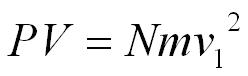
On average only a third of the molecules will be travelling in the direction we have chosen to focus on so,
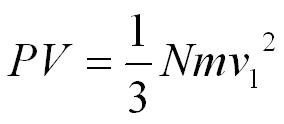
Molecules will be moving in different directions with different speeds so we will use the root mean square velocity (crms) to represent the average velocity of a molecule.